GA（遗传算法）求解TSP（旅行商问题）

TSP 问题（Travelling salesman problem）是组合优化中的一个 NP-hard 问题，在运筹学和理论计算机科学中具有十分重要的意义。该问题的主要内容为：给定一个城市列表和每对城市之间的距离，访问每个城市恰好一次并返回起始城市的最短路径是什么？
TSP 可以看作是一个图问题，即可以建模为一个无向加权图：
| 城市 | 路径 | 路径距离 |
| 顶点 | 边 | 边权 |
这是一个最小化问题，在访问彼此的顶点恰好一次后，从指定的顶点开始和结束。
该问题于1930年首次形式化，是优化中研究最深入的问题之一。许多优化方法都将其用作基准。虽然该问题计算难度大，但有大量的启发式和精确方法可用，因此可以完全解决数万个城市的问题，甚至可以在 1% 的误差范围内估计数百万个城市的问题。
即使是纯粹形式的TSP也有多种应用，例如规划、物流和芯片制造。这是很多领域的子问题，比如DNA测序。在这些应用中，“城市”的概念被用来表示客户、焊接点或 DNA 片段，而“距离”的概念则表示旅行时间或成本或 DNA 片段之间的相似性度量。TSP也用于天文学，天文学家在观察许多光源时希望减少在它们之间旋转望远镜所需的时间。在很多应用场景中，比如有限的资源或者时间窗口，可能需要额外的约束。
可以使用无向带权图对TSP进行建模，那么城市就是图的顶点，道路就是图的边，道路的距离就是边的长度。这是一个最小化问题，从特定顶点开始和结束，并且只访问每个顶点一次。通常，模型是一个完整的图（即每对顶点由一条边连接）。如果两个城市之间不存在路径，则添加一条很长的边可以完成图表，而不会影响最优环路的计算。
在对称TSP问题中，两个城市之间的距离相同，形成一个无向图。这种对称性将解决方案的数量减少了一半。在非对称TSP问题中，并非所有的双向路径都可能存在，或者来回距离不同，形成有向图。 交通事故、单行道、某些城市的出发和到达票价不同，都是打破这种对称性的例子。
GA(Genetic Algorithm)是计算数学中用于解决最优化问题的搜索算法，是进化算法的一种。该算法是一种受自然选择过程启发的元算法，是一种较大的进化算法类型（EA）。进化算法最初是借鉴进化生物学中的一些现象而发展起来的，包括遗传、突变、自然选择和杂交。

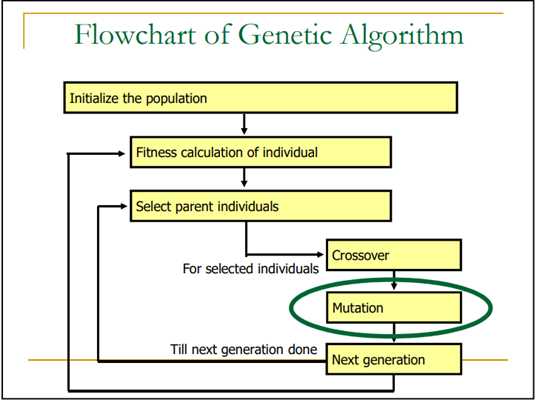
选择：从群体中选出优等个体并淘汰劣等个体的操作称为选择。
交叉：交叉是指将两个亲本个体的部分结构进行替换和重组以产生新个体的操作。
突变：变异算子的基本内容是改变种群中个体串某些位点的基因值。
路径表示是表示旅程对应的遗传密码的最自然和最简单的表示。 在编码、解码和存储过程中比较容易理解和实现。 例如：行程(5-1-7-8-9-4-6-2-3)可以直接表示为(5 1 7 8 9 4 6 2 3)。
（代码：https://github.com/yvonshong/Waseda/tree/master/Computational_Intelligence）
对该代码进行10000次迭代，其中一次的结果如下所示：


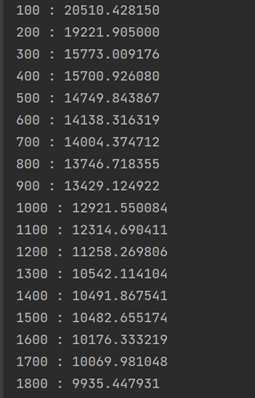
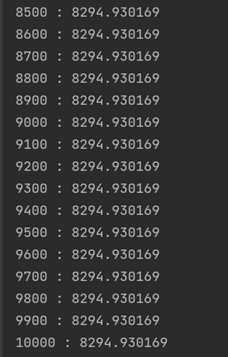
我们可以看到距离逐渐趋于稳定，趋于8294.930169，此即为本次运行的最优解。

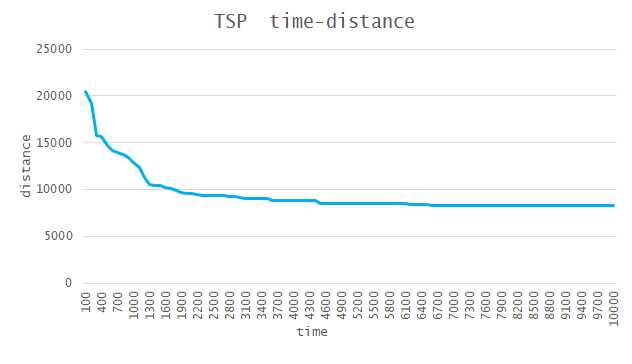
我们可以看到，随着代数的增加，距离逐渐接近8294.930169，然后逐渐变成水平的。
改进方案可以从crossrate和mutationrate这两个方面入手。 通过不断的运算，找出距离递减最快的crossrate和mutationrate，最终实现解的优化。